politopix
POLITOCAT AND POLITOPIX

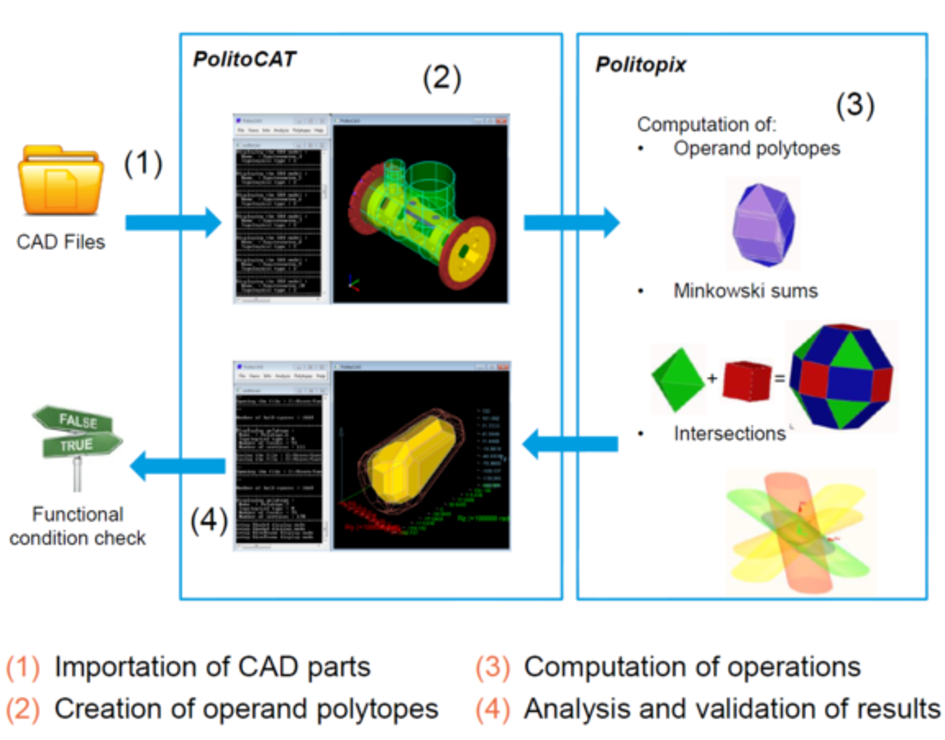
PolitoCAT: "Polytopes applied to Computer Aided Tolerancing"
- Download PolitoCAT v2.0.2 for Windows64 and install it directly at the root of your hard disk C: providing 1.4 Go of free space. PolitoCAT is a free software under the GNU LGPL license, with a kernel based on politopix and a graphical interface. This is the first contribution to the AToPAd project.
- Download the PolitoCAT tutorial v2.0.0 written by C. Restrepo & al.
- Download PolitoCAT v1.2.8 for Windows and install it directly at the root of your hard disk C: providing 600 Mo of free space. PolitoCAT is a free software under the GNU LGPL license, with a kernel based on politopix and a graphical interface.
- Download the PolitoCAT tutorial v1.2.8 written by S. Arroyave
- Download the presentation made in the E-GRT 2015 (European Group of Research in Tolerancing) in Erlangen, Germany
Politopix
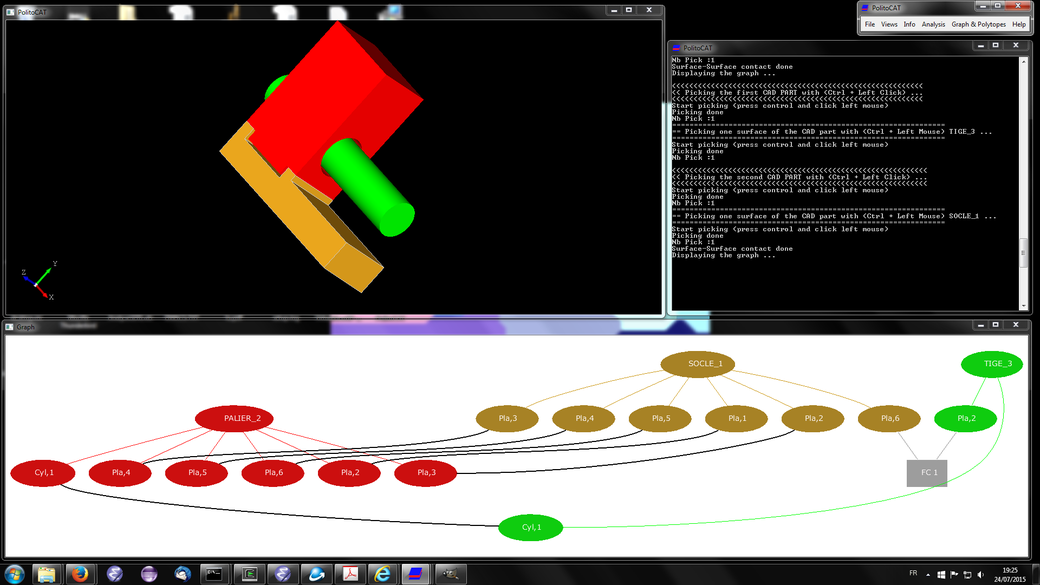
To study the cumulative stack-up of geometric variations inside any mechanical system we need to compute Minkowski sums and intersections of sets of contraints modelled by polytopes in R6. As a consequence, we developped the solver politopix under the GNU GPL license (if you need a specific license fitting your needs please contact V. Delos) and its documentation.
- Download the NEW politopix version 5.0.0 to compile under Windows and Linux
- Download the 64-bit Windows executable politopix.exe version 4.2.0 with polito.dll
- Download the slides presenting politopix (CERN, Geneva june 2014)
Team
- Software & library project manager (architecture, coding/integration, tests, versioning and deployment): V. Delos
- Tolerancing analysis, 3D visualization and attribute management: D. Teissandier
- Tolerancing analysis, coding of industrial cases and test suites: S. Garcia y Gomez, C. Restrepo y Garcia, S. Arroyave-Tobon and Doriane Gouyou
Theory of the Minkowski Sums of polytopes
- Download the presentation of Minkowski sum of HV-polytopes in Rn (Singapore, CMCGS January 2015)
- Download the presentation of Minkowski sum of polytopes defined by their vertices (Shanghai, GTA2015, January 2015) and the source code to compile with GLPK
Minkowski sums and intersection of polytopes with politopix
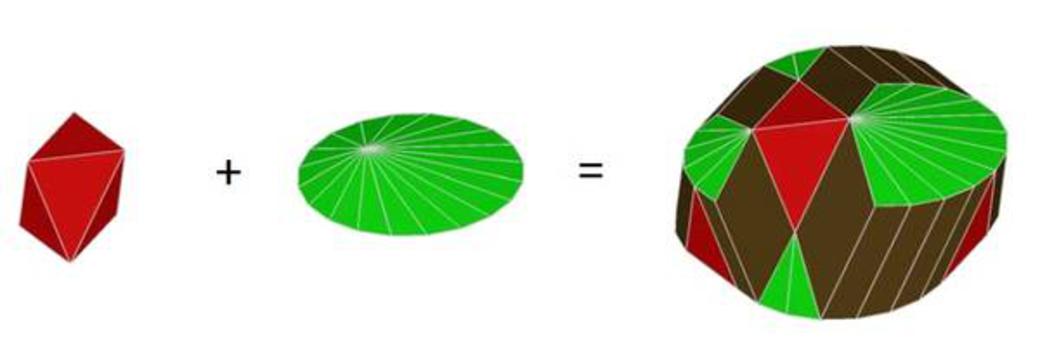
politopix allows you to sum and intersect polytopes or polyhedrical cones in a n-dimensional space. Its applications are dedicated to geometric tolerancing and industrial mechanics. politopix can also compute n-dimensional Voronoi diagrams.
Sum in R6 checking the topology and geometry of the result:
./politopix.exe -p1 Polytope_1.ptop -p2 Polytope_2.ptop -d 6 -MS -ch
Intersection of cones in R6:
./politopix.exe -c1 cone_1.pcon -c2 cone_2.pcon -d 6 -ch
Workshop
Studying polyhedral properties in geometric tolerancing, 24 – 28 April, 2023, CIRM (Marseille, France)
In mechanical engineering, the manufacturing processes of the parts in a mechanical system generate geometric deviations with respect to a nominal or perfect model created thanks to a Computer Aided Design tool. These deviations can strongly damage the behaviour of the mechanism. Geometric tolerancing has to predict if these deviations are acceptable according to the mechanism specifications. In the – very simple – case where we stack up cubes, the upper face wil never be perfectly parallel to the bottom one. So we have to be able to compute, according to the given manufacturing tolerances and contacts between cubes, the set of positions that can take the upper face with respect to the lower one. The operation Minkowski sum of polyhedra can model the total cumulative deviations through the mechanism, and the intersection deal with the multiple contacts between parts. The first algorithms able to process all the mechanisms came out from the laboratory I2M (UMR CNRS 5295). There are very numerous applications in the world of research (particle accelerator, detector, spectrometre,…) and industry (aeronautics, spatial, automotive, railway). However, there are still a lot of opened topics dealing with this polyhedral approach in a n-dimensional space. The originality of the works developed in I2M, backed by researchers from the LPSM (UMR CNRS 8001), is that we formalize geometric tolerancing through polyhedral operations.
Awards
- Best paper of the 36th Computers and Information in Engineering Conference – Advanced Modeling & Simulation, Charlotte, USA, 21-24 August 2016, American Society of Mechanical Engineering
- Prix de la Recherche partenariale 2020 de l’Institut Carnot ARTS, a French research institute grouping together the 23 laboratories of the engineering school Arts et Métiers ParisTech
Contacts
DENIS TEISSANDIER
I2M UMR CNRS 5295 Arts et Métiers ParisTech
I2M UMR CNRS 5295 Arts et Métiers ParisTech
Esplanade des Arts et Métiers
33405 TALENCE
05 56 84 63 93
Contacter par courriel
VINCENT DELOS
I2M UMR CNRS 5295 Arts et Métiers ParisTech
Esplanade des Arts et Métiers
33405 Talence
05 56 84 53 33 poste 54 51
Contacter par courriel







